Study area
This European analysis includes 40 continental states, 27 of which are member states of the EU. The study area comprises almost all European countries, except for seven (Vatican, Iceland, Belarus, Ukraine, Republic of Moldova, and transcontinental states Russia and Turkey) that were not included in the study, due to small size (Vatican, without agricultural areas) or lack of geospatial data for most of the analysed land degradation processes (in the remaining six countries). The 40 countries total an area of ~5 million (M) km2 (approximately half of the European continent) and hold a combined agricultural area of ~2.10 M km2 (~42% of the total area), over half of which (~1.14 M km2) consists of arable areas.
Data selection
In order to investigate land multi-degradation in Europe, we selected twelve processes that are highly representative for agricultural environments (Table 2). The twelve processes are the most relevant for highlighting the agricultural landscapes’ degradation in Europe (and worldwide)2, considering certain bio-physical mechanisms, general or particular, that trigger various negative effects in land productivity (Table 2). Several suggestive examples of such disruptive effects, which lead to the decrease or loss of land agro-ecological productivity, were documented for each degradation process, based on specialised literature (Table 2).
Data acquisition/preparation
For the selected processes, we acquired/processed twelve geospatial databases. Essentially, we collected databases that were already available in their final form for six LD processes, the detailed processing information of which can be found directly in data sources – water erosion11, soil organic carbon loss19, soil salinization30, soil acidification31, soil compaction32 and soil pollution via pesticides29 (Table 3). For the other layers, we used various pre-existent data from other data sources, in order to refine (wind erosion) or model/obtain (soil nutrient imbalances, soil pollution via heavy metals, vegetation degradation, groundwater decline and aridity) the final data for the remaining six processes (Table 3).
Wind erosion was predicted by physically-based modelling of the aeolian sediment transport (Q) for a given particle size. The Q is controlled mainly by two key properties: the momentum of the wind and the wind friction, influenced mainly by vegetation, which reduces the momentum reaching the unsheltered soil surface. The soil surface characteristics limit the entrainment of dry, loose, and available sediment, resulting in a specific threshold. That threshold is increased by soil moisture, which inhibits entrainment and for which a function is available. The availibility of sediment is limited by biogeochemical soil crusts/seals, but no parameterisations are currently available. Consequently, sediment is assumed to have an infinite supply and Q is limited only by the ability of wind friction to exceed the entrainment threshold. Finally, for a given pixel we converted the one-dimensional Q (g m–1 s–1) to an areal wind erosion (g m–2 s–1, subsequently converted to t ha–1 yr–1) by dividing by the length scale of the pixel. Details about the Q modelling and the data layers used can be found in Chappell et al.13. For this study, we reprocessed the data of that original study so that we could export high-resolution (500 m) data for use in the subsequent analyses with other degradation processes (Table 3).
Soil nutrient imbalances were obtained based on geospatial data on nitrogen (N, in kg/ha) and phosphorus (P, in mg/kg) soil content and flows, which allowed to identify N and P surplus (that can indicate, for instance, the risk of pollution through overfertilization) and deficit (a likely decrease in land productivity) conditions (Table 3). For N, the first step involved the identification of an operative safe space as illustrated by Quemada et al.33, beyond which environmental impacts may arise from both 1) excessive N surplus (that is N input – crop export), leading to detrimental losses to air and water, and 2) very high N use efficiency (NUE, that is the ratio between crop export and N inputs) that can mine soil fertility and reduce the productivity. According to Quemada et al.33. and expert opinions, we defined an operative N safe space having NUE 34,35 extended at 1 km gridded level. Therefore, N imbalance was defined in this research as having surplus (>50 kg/ha) or NUE ( > 0.9) deficit (Table 3).
For the P data, we combined both the soil available P and budget (P input – export by crops) to define P imbalance conditions, since sorption/desorption processes vary widely in different soils, making the available P only an approximate indicator of P status (due to also legacy effects and its low reactivity in soil). Basically, we defined two P conditions that can threaten the agricultural land productivity, namely 1) a surplus level, when P available in soil is >50 mg/kg and there is a positive budget, and 2) a deficit condition, when P is 36,37 (Table 3). After separately classifying N and P raster data, the four resulting classes were merged as a single raster with soil nutrient imbalances, which is itself can be considered an important facet of LD.
Soil pollution via heavy metals was processed using separate raster data of nine toxic substances (As, Cd, Cr, Co, Pb, Sb, Ni, Cu, and Hg, with values in mg/kg) that were spatially predicted in Europe38,39,40. The nine rasters, generated in several data sources based on Land Use/Land Cover Area Frame Survey (LUCAS) topsoil database41 and other auxiliary data38,39,40, were first classified using some critical thresholds proposed for each harmful substance (Table 3). Subsequently, heavy metal soil pollution was processed as a single layer by joining/intersecting the individual rasters with delimited critical concentrations in topsoils. Selecting European areas with high concentrations of heavy metals, above the standard guideline thresholds of toxic elements38,42 (Table 3), was essential for highlighting soil contamination, which is a threat to soil-based ecosystem services.
The vegetation degradation raster was obtained based on Normalized Difference Vegetation Index (NDVI) data, extracted and converted as annual values from the Moderate Resolution Imaging Spectroradiometer (MODIS) Terra MOD13A1 product43. This process was examined using the Mann-Kendall (MK) test44,45 and Sen’s slope estimator46,47 in the analysis of annual NDVI trends, at pixel level (Table 2). Vegetation degradation was detected based on negative NDVI trends (which can define the areas with agricultural vegetation affected by devitalization, decreases in density/consistency or biomass decline), identified as statistically significant at the p-value ≤ 0.1 (a threshold that includes strong significant trends, for p-values p-values between 0.05 to 0.1)48 (Table 3).
The groundwater decline modelling was based on groundwater table depth (GTD, in m) simulated using a global hydrology model49, at ~1-km grid size and 1-hour time steps over 10 years (Table 2), driven by observed vegetation biomass (Leaf Area Index from MODIS) and European Centre for Medium Range Weather Forecast (ECMWF) ERA5 reanalysis atmosphere50. The model simulates soil water infiltration solving the 1D Richards’ equation in columns discretized with 40 layers that get thicker with depth, down to 1 km deep. It includes groundwater dynamics, with the water table being the lower boundary condition of the soil columns. Vertically integrated groundwater lateral flows are calculated based on Darcy’s law, driven by water table horizontal gradients. The model represents the 2-way exchange between groundwater and rivers or wetlands, river flow and inundation, and dynamic plant root uptake49. The model has been validated with flux tower observations of evapotranspiration and gage observations of stream flow. The model output was saved at monthly GTD values, but averaged here into annual values for detecting trends over a decade, using the MK test44,45 and Sen’s slope estimator46,47 (Table 3). The two statistical procedures were applied for detecting negative GTD pixel trends (which can suggest depleting or decreasing groundwater resources, with negative consequences for agricultural plant growth), statistically significant at the p-value ≤ 0.1 confidence level (Table 3).
The last raster layer, of aridity, was processed by computing an Aridity Index (AI, in mm/mm) (Table 3) based on mean multiannual precipitation (P, in mm) and potential evapotranspiration (PET, in mm) data, extracted from CHELSA (Climatologies at high resolution for the earth’s land surface areas) database51,52. The Aridity Index, calculated as a ratio between the two climatic parameters (AI = P/PET), defines four types of drylands (lands affected by aridity) below the 0.65 mm/mm threshold – dry sub-humid (AI values between 0.65 and 0.5 mm/mm), semi-arid (0.5–0.2 mm/mm), arid (0.2–0.03 mm/mm) and hyper-arid (2,53. In Europe, the aridity layer was produced based on dry sub-humid, semi-arid, and arid climate conditions, the presence of which on the continent can limit agricultural productivity through constant dryness or climate-induced desertification.
Final data modelling
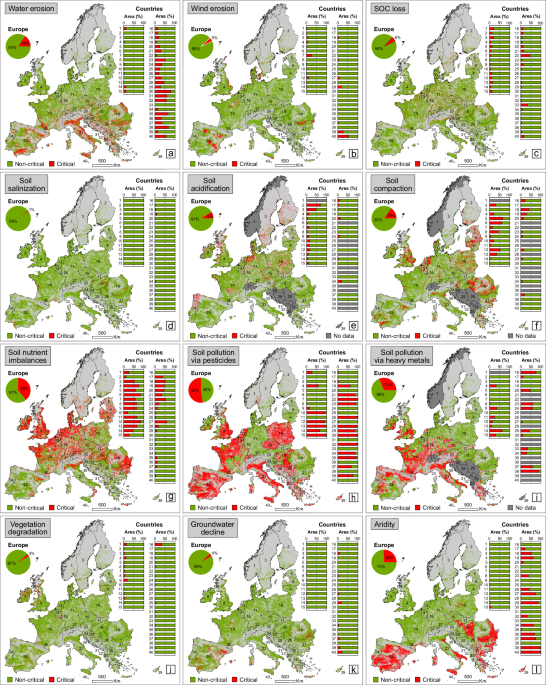
All 12 collected/processed spatial databases were finally processed at 500 m (an approximately intermediate spatial resolution in the variety of the original data resolution) (Table 3) and were structured/prepared into 2 general classes, named “Non-critical” and “Critical” (Fig. 1). The “Critical” class of each examined process was mapped using critical thresholds documented in literature, over/under which each LD process triggers the reduction/loss of agricultural land productivity (Table 3). In addition to the rigorous documentation from scientific literature, the critical thresholds were defined according to environmental criteria for healthy/unhealthy soil conditions (most notably for soil erosion, soil salinization, loss of soil organic carbon, and soil compaction), reported in the draft of the Soil Monitoring Law proposed by the European Commission (on July 5th, 2023) and currently under discussion in the European Parliament54.
The “Critical” class, which highlights high/severe degradative conditions in agricultural landscapes (Table 3), was included in the final spatial data modelling, in order to obtain a relevant indicator for the continental assessment of multiple and convergent LD pathways. More specifically, by superimposing/intersecting the 12 datasets, we obtained the Land Multi-degradation Index (LMI), which indicates the simultaneous presence (co-occurrence) of degradative processes, at the pixel level. LMI (500 m pixel size) was processed strictly at the level of the agricultural boundaries in Europe, which were extracted from the CORINE Land Cover (CLC) database, 2018 edition (the most up-to-date)55. The CLC dataset used here includes four general agricultural classes, namely arable land (2.1.1, 2.1.2, and 2.1.3 codes in the CLC nomenclature), permanent crops (2.2.1, 2.2.2, 2.2.3), pastures (2.3.1) and heterogeneous agricultural areas (2.4.1, 2.4.2, 2.4.3, 2.4.4)55.
LMI has been investigated at the level of all agricultural classes, but also strictly within arable lands, to emphasize the co‐occurrence pattern of processes in the most important agricultural environments for European food security. Also, this index was processed in all 40 countries, despite the fact that for 3 processes (soil acidification, soil compaction, and soil pollution via heavy metals) there was no geospatial data for Norway, Switzerland, Balkan countries, Cyprus, and Malta (Fig. 1) (for these countries, in the Supplementary Information section, LMI was obtained based on the 9 remaining processes with available data).
Finally, LMI was investigated and interpreted based on five general classes, which emphasized very low (a single process present at pixel level), low (co-occurrence of 2 LD processes), medium (3), high (4) and very high (≥5) degradative conditions in agricultural/arable lands (Fig. 2). We set these classes considering the LMI histogram (in which a data distribution of >90% condensed in the interval 1 to 5 synergistic processes was observed) (Fig. 2b,e), the natural breaks classification method56 – which revealed roughly similar classes, but also the LMI value arithmetic mean, which showed just over 2 co-occurring processes in Europe (close to an intermediate value in the 1–5 interval used to set LMI classes). In addition to the 3 statistical criteria considered simultaneously, we set the 5 classes also with the aim to obtain an easy/fast interpretation of the LMI. All data processing and graphic analyses of this study were performed using various software, like R-package57, ArcGIS58, or Inkscape59.
Data quality and limitations
The quality of this study’s data can be evaluated via three key aspects. Firstly, the reliability of the 6 datasets directly acquired is supported by the published studies referenced in this paper (data source indicated for processes no. 1, 3, 4, 5, 6, and 8, in Table 3), where uncertainties and errors were generally addressed. Secondly, we considered the quality of the data for the other 6 processes modelled here, by using reliable pre-existent data (input data of processes no. 2, 7, 9, 10, 11, and 12, which were also checked in the sources featured in Table 3, in terms of uncertainties and errors) in obtaining the final geospatial layers. Thirdly, for the 2 layers created in this study (no. 10 and 11 in Table 3), we exclusively selected statistically significant trends, which limits uncertainties/errors in these particular cases.
Some potential limitations may exist in our methodological approach. These may emerge from the different spatial/temporal resolution (1) and metrics (2) of the geospatial data, from the choice in thresholds that define “Critical” classes of the twelve processes (3), from assigning equal contributions to all layers in computing LMI (4), or from integrating only 75–83% of all input layers for LMI computation (Supplementary Information), in the case of some European countries (5). In the first case (1), it would have been ideal to use datasets with similar/identical spatial and temporal resolutions, which was however impossible, given the high number of data layers used, with different technical (pixel size and time periods) characteristics available in the literature (Table 3).
In the second instance (2), it would have been better if soil compaction and soil pollution via pesticides had a quantitative nature (similarly to all the other 10 databases), instead of a qualitative (adimensional) measurement unit (Table 3), but in the case of the two processes we were constrained by the unavailability of other (quantitative) data in literature. Also, another (apparent) shortcoming on this second point could be linked to the geospatial layers that were obtained based on some multi-temporal data, but which were interpreted based on different metrics. More precisely, vegetation degradation and groundwater decline were assessed as LD pathways based on negative annual trends (as per the reasoning presented in the section dedicated to data acquisition/preparation), while the aridity layer was examined through a mean multiannual ratio (of climate data) (Table 3). However, we argue this choice is more appropriate, as the mere presence of aridity conditions (and not necessarily the intensification of this process, which could have been detected based on geostatistical trends) is sufficient to trigger some major drivers of degradation, like desertification3.
In the third case (3), the critical thresholds of some factors may be debated – e.g. severe erosion rates60 are considered as those exceeding the threshold of 10 t ha–1 yr–1, while in other studies8,61, the unsustainable level of this process (examined in the long term in relation to soil formation rates) is adjusted to >2 t ha–1 yr–1, the threshold selected in this research (Table 3). Since our applied methodology required choosing a unique critical threshold for each layer of degradation, we eventually set “Critical” classes by consulting a high number of relevant papers and scientific reports (only a few of which were exemplified in this study), which supported the thresholds selected for this approach (Table 3).
In the fourth case (4), we attributed equal importance to all drivers of degradation, although in reality, some processes (e.g. soil salinization) could trigger more severe effects in the decrease of agricultural productivity, compared to other degradative factors (e.g. vegetation degradation). However, we avoided a weighting of the factors in modelling LMI, considering that, in principle, each process can lead to multiple negative effects for land productivity (Table 2), especially since it is almost impossible to determine the exact impact of each process in the land multi-degradation mechanism.
Finally (5), due to the unavailability of geospatial data, we omitted up to 25% (three LD processes – soil acidification, soil compaction, soil pollution via heavy metals) of all input layers used to model LMI results, which were presented in detail (for all 40 countries) in the Supplementary Information section. Nevertheless, these missing data affected (potentially underestimated) LMI results in the case of a limited number of European countries (Supplementary Figs. 2–4 and Supplementary Tables 1–13), i.e. the Balkan states, Switzerland, Norway (with all three processes not integrated in the LMI, but still with three-quarters of all databases available to obtain the final results of land multi-degradation) and, partially, Cyprus and Malta (only two processes missing – soil acidification and soil pollution via heavy metals) (Fig. 1).
Data uncertainty and sensitivity
To assess the effect of varying thresholds on the binary classification adopted to obtain the LMI map (which was a crucial methodological phase of our approach), an uncertainty and sensitivity analysis was performed. More specifically, through an operation of layer stacking, the multiple data used to derive the twelve LD binary layers (maps) were combined in a single matrix of original inputs. For each of one the input maps, random simulations (n = 20,000) were adopted by varying the threshold initially set and using values drawn from a normal distribution, with the numerical value of the threshold as the mean and a value of one-tenth of the threshold as standard deviation. The matrix was then reclassified into binary classes according to the thresholds randomly defined. Subsequently, the row values were summed up to obtain the LMI values under different thresholds. Given the reclassification step, the LMI still varied from 0 to 10, but in some of the rows, its values (under the same initial conditions) might have varied due to the different classification.
Finally, the LMI values derived were used as a dependent variable in a Random Forest (RF) classification model (1000 decision trees and 20 repetitions)62 that was applied in a R statistics enviroment63, using the initial input maps as covariates. The RF model was used for its ability to produce classification probabilities (so predicting with which probability a pixel falls within a given class), thus providing an estimate of how much varying threshold results in a different final classification (Supplementary Fig. 1). Moreover, the RF results obtained (Supplementary Fig. 1) can be leveraged to assess how much each of the initial variables influences the classification, consequently offering a valuable sensitivity analysis for our LMI findings.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.